Algorithm About Queue

Posted on:March 12, 2023 at 01:39 AM
Share on

It’s about the data struct of linear — queue and the Algorithm on it.

Table of contents

Open Table of contents

队列(queue) && 双端队列(deque)

Last in - Last out First in - First out

队列的关键点

操作复杂度

优先队列(priority queue)

优先队列的关键点

操作复杂度

Note: 插入：一般是 O(logN)(二叉堆)，一些高级数据结构可以做到 O(1)(配对堆，斐波那契堆)

Java JDK

实战

  1. Implement Stack using Queues

Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (push, top, pop, and empty).

Implement the MyStack class:

Notes:

Example 1:

Input
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
Output
[null, null, null, 2, 2, false]

Explanation
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // return 2
myStack.pop(); // return 2
myStack.empty(); // return False

Constraints:

Follow-up: Can you implement the stack using only one queue?

class MyStack {
    Queue<Integer> queue1;
    Queue<Integer> queue2;

    public MyStack() {
        queue1 = new LinkedList();
        queue2 = new LinkedList();
    }

    public void push(int x) {
        queue2.offer(x);
        while(!queue1.isEmpty()){
            queue2.offer(queue1.poll());
        }
        Queue<Integer> temp = queue2;
        queue2 = queue1;
        queue1 = temp;
    }

    public int pop() {
       return queue1.poll();
    }

    public int top() {
       return queue1.peek();
    }

    public boolean empty() {
        return queue1.isEmpty();
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

思路

  1. Design Circular Queue

Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called “Ring Buffer”.

One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.

Implement the MyCircularQueue class:

Example 1:

Input
["MyCircularQueue", "enQueue", "enQueue", "enQueue", "enQueue", "Rear", "isFull", "deQueue", "enQueue", "Rear"]
[[3], [1], [2], [3], [4], [], [], [], [4], []]
Output
[null, true, true, true, false, 3, true, true, true, 4]

Explanation
MyCircularQueue myCircularQueue = new MyCircularQueue(3);
myCircularQueue.enQueue(1); // return True
myCircularQueue.enQueue(2); // return True
myCircularQueue.enQueue(3); // return True
myCircularQueue.enQueue(4); // return False
myCircularQueue.Rear();     // return 3
myCircularQueue.isFull();   // return True
myCircularQueue.deQueue();  // return True
myCircularQueue.enQueue(4); // return True
myCircularQueue.Rear();     // return 4

Constraints:

class MyCircularQueue {
    private int capacity;
    private int[] element;
    private int front;
    private int rear;

    public MyCircularQueue(int k) {
        capacity = k+1;
        element = new int[capacity];
        front = 0;
        rear = 0;
    }

    public boolean enQueue(int value) {
        if(isFull()){
            return false;
        }
        element[rear] = value;
        rear = (rear + 1) % capacity;
        return true;
    }

    public boolean deQueue() {
        if(isEmpty()){
            return false;
        }
        front = (front + 1) % capacity;
        return true;
    }

    public int Front() {
        if(isEmpty()){
            return -1;
        }
        return element[front];
    }

    public int Rear() {
        if(isEmpty()){
            return -1;
        }
        return element[(rear - 1 + capacity)%capacity];
    }

    public boolean isEmpty() {
        return front == rear;
    }

    public boolean isFull() {
        return (rear + 1)% capacity == front;
    }
}

/**
 * Your MyCircularQueue object will be instantiated and called as such:
 * MyCircularQueue obj = new MyCircularQueue(k);
 * boolean param_1 = obj.enQueue(value);
 * boolean param_2 = obj.deQueue();
 * int param_3 = obj.Front();
 * int param_4 = obj.Rear();
 * boolean param_5 = obj.isEmpty();
 * boolean param_6 = obj.isFull();
 */

思路：

我们可以通过一个数组进行模拟，通过操作数组的索引构建一个虚拟的首尾相连的环。在循环队列结构中，设置一个队尾 rear 与队首 front，且大小固定，结构如下图所示:

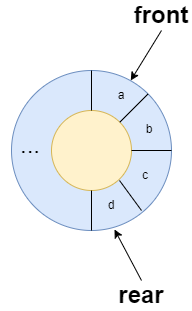
在循环队列中，当队列为空，可知 front=rear；而当所有队列空间全占满时，也有 front=rear。为了区别这两种情况，假设队列使用的数组有 capacity 个存储空间，则此时规定循环队列最多只能有 capacity−1 个队列元素，当循环队列中只剩下一个空存储单元时，则表示队列已满。根据以上可知，队列判空的条件是 front=rear，而队列判满的条件是front=(rear+1)%capacity。 对于一个固定大小的数组，只要知道队尾 rear 与队首 front，即可计算出队列当前的长度：(rear−front+capacity)%capacity。

循环队列的属性如下:

循环队列的接口方法如下：

  1. Design Circular Deque

Design your implementation of the circular double-ended queue (deque).

Implement the MyCircularDeque class:

Example 1:

Input
["MyCircularDeque", "insertLast", "insertLast", "insertFront", "insertFront", "getRear", "isFull", "deleteLast", "insertFront", "getFront"]
[[3], [1], [2], [3], [4], [], [], [], [4], []]
Output
[null, true, true, true, false, 2, true, true, true, 4]

Explanation
MyCircularDeque myCircularDeque = new MyCircularDeque(3);
myCircularDeque.insertLast(1);  // return True
myCircularDeque.insertLast(2);  // return True
myCircularDeque.insertFront(3); // return True
myCircularDeque.insertFront(4); // return False, the queue is full.
myCircularDeque.getRear();      // return 2
myCircularDeque.isFull();       // return True
myCircularDeque.deleteLast();   // return True
myCircularDeque.insertFront(4); // return True
myCircularDeque.getFront();     // return 4

Constraints:

class MyCircularDeque {

    // 1、不用设计成动态数组，使用静态数组即可
    // 2、设计 head 和 tail 指针变量
    // 3、head == tail 成立的时候表示队列为空
    // 4、tail + 1 == head
    private int capacity;
    private int[] arr;
    private int front;
    private int rear;

    public MyCircularDeque(int k) {
        capacity = k+1;
        arr = new int[capacity];
        // 头部指向第 1 个存放元素的位置
        // 插入时，先减，再赋值
        // 删除时，索引 +1（注意取模）
        front = 0;
        // 尾部指向下一个插入元素的位置
        // 插入时，先赋值，再加
        // 删除时，索引 -1（注意取模）
        rear = 0;
    }

    public boolean insertFront(int value) {
        if(isFull()){
            return false;
        }
        front = (front -1 + capacity) % capacity;
        arr[front] = value;
        return true;
    }

    public boolean insertLast(int value) {
        if(isFull()){
            return false;
        }
        arr[rear] = value;
        rear = (rear + 1) % capacity;
        return true;
    }

    public boolean deleteFront() {
        if(isEmpty()){
            return false;
        }
        // front 被设计在数组的开头，所以是 +1
        front = (front + 1) % capacity;
        return true;
    }

    public boolean deleteLast() {
        if(isEmpty()){
            return false;
        }
        // 被设计在数组的末尾，所以是 -1
        rear = (rear - 1 + capacity) % capacity;
        return true;
    }

    public int getFront() {
        if(isEmpty()){
            return -1;
        }
        return arr[front];
    }

    public int getRear() {
        if(isEmpty()){
            return -1;
        }
        // 当 rear 为 0 时防止数组越界
        return arr[(rear - 1 + capacity) % capacity];
    }

    public boolean isEmpty(){
        return front == rear;
    }

    public boolean isFull(){
        // 注意：这个设计是非常经典的做法
        return (rear + 1) % capacity == front;
    }
}

/**
 * Your MyCircularDeque object will be instantiated and called as such:
 * MyCircularDeque obj = new MyCircularDeque(k);
 * boolean param_1 = obj.insertFront(value);
 * boolean param_2 = obj.insertLast(value);
 * boolean param_3 = obj.deleteFront();
 * boolean param_4 = obj.deleteLast();
 * int param_5 = obj.getFront();
 * int param_6 = obj.getRear();
 * boolean param_7 = obj.isEmpty();
 * boolean param_8 = obj.isFull();
 */

思路：

根据循环队列的定义，队列判空的条件是 front=rear，而队列判满的条件是front=(rear+1)%capacity,对于一个固定大小的数组，只要知道队尾 rear与队首front，即可计算出队列当前的长度：(rear−front+capacity)%capacity.循环双端队列与循环队列的属性一致:

循环双端队列的接口方法如下：

Share on