Algorithm About Hash

Posted on:March 13, 2023 at 03:34 PM
Share on

It’s about the data struct of linear — hash and the Algorithm on it.

Table of contents

Open Table of contents

哈希表

希表的关键点

哈希碰撞

无序集合

集合的特点和分类

映射的特点和分类

实战

  1. Two Sum

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.

Example 1:

Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2:

Input: nums = [3,2,4], target = 6
Output: [1,2]

Example 3:

Input: nums = [3,3], target = 6
Output: [0,1]

Constraints:

Follow-up: Can you come up with an algorithm that is less than O(n2) time complexity?

class Solution {
    Map<Integer,Integer> numsMap = new HashMap();
    public int[] twoSum(int[] nums, int target) {
        for (int i =0;i< nums.length;i++){
            int num = nums[i];
            int otherNum = target - num;
            if(numsMap.containsKey(otherNum)){
                return new int[]{numsMap.get(otherNum),i};
            }
            numsMap.put(num,i);
        }
        return null;
    }
}
  1. Walking Robot Simulation

A robot on an infinite XY-plane starts at point (0, 0) facing north. The robot can receive a sequence of these three possible types of commands:

Some of the grid squares are obstacles. The ith obstacle is at grid point obstacles[i] = (xi, yi). If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.

Return the maximum Euclidean distance that the robot ever gets from the origin squared (i.e. if the distance is 5, return 25).

Note:

Example 1:

Input: commands = [4,-1,3], obstacles = []
Output: 25
Explanation: The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.

Example 2:

Input: commands = [4,-1,4,-2,4], obstacles = [[2,4]]
Output: 65
Explanation: The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.

Example 3:

Input: commands = [6,-1,-1,6], obstacles = []
Output: 36
Explanation: The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.

Constraints:

import java.util.HashSet;
import java.util.Set;

class Solution {
   public int robotSim(int[] commands, int[][] obstacles) {
        Set<Long> obs = new HashSet();
        int ans = 0;
        // change the barrier to set, so it can be find in o(1)
        for (int[] obstacle : obstacles) {
            // obs.add(obstacle[0]+","+obstacle[1]);
            // get hash with long is faster then the string
            obs.add(calcHash(obstacle));
        }

        // init the original positions
        int x = 0, y = 0;
        // init the direction, 0 for north;1 for east; 2 for south and 3 for west
        int dir = 0;

        // init a direction array, when walk to north the dx= 0 and dy = 1, and so on
        int[] dx = new int[]{0, 1, 0, -1};
        int[] dy = new int[]{1, 0, -1, 0};

        // deal with the commends
        // -2: Turn left 90 degrees.
        // -1: Turn right 90 degrees.
        // 1 <= k <= 9: Move forward k units, one unit at a time.
        for (int command : commands) {
            if (command == -1) {
                dir = (dir + 1) % 4;
            } else if (command == -2) {
                dir = (dir - 1 + 4) % 4;
            } else {
                for (int i = 0; i < command; i++) {
                    // calc the next position
                    int nx = x + dx[dir];
                    int ny = y + dy[dir];
                    // deal with the barrier
                    //if (obs.contains(calcHash(nx+","+ny))) break;
                    if (obs.contains(calcHash(new int[]{nx,ny}))) break;
                    x = nx;
                    y = ny;
                    ans = Math.max(ans, x * x + y * y);
                }
            }
        }

        return ans;
    }

    long calcHash(int[] obstacle){
        // as unique key, use the row*i + column, add the number for transform it to a non-negative number
        return (obstacle[0]+ 30000l) * 60001l + (obstacle[1] + 30000l);
    }
}

本题可以抽象出对于方向数组的模板运用，其思路有点类似循环队列，此模板有以下几个关键点：

设定初始的朝向枚举值：int dir = 0; // N=0, E=1, S=2, W=3 设定不同朝向下，具体的行进路径

int[] dx = new int[]{0, 1, 0, -1};
int[] dy = new int[]{1, 0, -1, 0};

利用求余数的思路，在四个朝向中快速做转换

if (command == -1) {
    dir = (dir + 1) % 4;
} else if (command == -2) {
     dir = (dir - 1 + 4) % 4;
}

利用哈希表（自定义哈希函数），提供障碍物的检索能力

  1. Subdomain Visit Count

A website domain “discuss.leetcode.com” consists of various subdomains. At the top level, we have “com”, at the next level, we have “leetcode.com” and at the lowest level, “discuss.leetcode.com”. When we visit a domain like “discuss.leetcode.com”, we will also visit the parent domains “leetcode.com” and “com” implicitly.

A count-paired domain is a domain that has one of the two formats “rep d1.d2.d3” or “rep d1.d2” where rep is the number of visits to the domain and d1.d2.d3 is the domain itself.

For example, “9001 discuss.leetcode.com” is a count-paired domain that indicates that discuss.leetcode.com was visited 9001 times. Given an array of count-paired domains cpdomains, return an array of the count-paired domains of each subdomain in the input. You may return the answer in any order.

Example 1:

Input: cpdomains = ["9001 discuss.leetcode.com"]
Output: ["9001 leetcode.com","9001 discuss.leetcode.com","9001 com"]
Explanation: We only have one website domain: "discuss.leetcode.com".
As discussed above, the subdomain "leetcode.com" and "com" will also be visited. So they will all be visited 9001 times.

Example 2:

Input: cpdomains = ["900 google.mail.com", "50 yahoo.com", "1 intel.mail.com", "5 wiki.org"]
Output: ["901 mail.com","50 yahoo.com","900 google.mail.com","5 wiki.org","5 org","1 intel.mail.com","951 com"]
Explanation: We will visit "google.mail.com" 900 times, "yahoo.com" 50 times, "intel.mail.com" once and "wiki.org" 5 times.
For the subdomains, we will visit "mail.com" 900 + 1 = 901 times, "com" 900 + 50 + 1 = 951 times, and "org" 5 times.

Constraints:

class Solution {
    public List<String> subdomainVisits(String[] cpdomains) {
        Map<String,Integer> counts = new HashMap<>();
        for(String domain: cpdomains){
            String[] cpinfo = domain.split("\\s+");
            String[] frags = cpinfo[1].split("\\.");
            int count = Integer.valueOf(cpinfo[0]);

            String cur = "";
            for(int i = frags.length - 1; i >= 0; i--){
                cur = frags[i] + (i < frags.length - 1?".":"") + cur;
                counts.put(cur, counts.getOrDefault(cur,0) + count);
            }
        }

        List<String> ans = new ArrayList<>();
        for(String dom: counts.keySet()){
            ans.add(counts.get(dom)+" "+ dom);
        }
        return ans;
    }
}
  1. Degree of an Array

Given a non-empty array of non-negative integers nums, the degree of this array is defined as the maximum frequency of any one of its elements.

Your task is to find the smallest possible length of a (contiguous) subarray of nums, that has the same degree as nums.

Example 1:

Input: nums = [1,2,2,3,1]
Output: 2
Explanation:
The input array has a degree of 2 because both elements 1 and 2 appear twice.
Of the subarrays that have the same degree:
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
The shortest length is 2. So return 2.

Example 2:

Input: nums = [1,2,2,3,1,4,2]
Output: 6
Explanation:
The degree is 3 because the element 2 is repeated 3 times.
So [2,2,3,1,4,2] is the shortest subarray, therefore returning 6.

Constraints:

class Solution {
    public int findShortestSubArray(int[] nums) {
        Map<Integer,int[]> infos = new HashMap<>();
        int count = 0;
        int minLen = nums.length;
        for(int i=0; i<nums.length; i++){
            if(!infos.containsKey(nums[i])){
                // if the nums not exsit, update the first position and count
                infos.put(nums[i],new int[]{1,i,i});
            }else{
                int[] info = infos.get(nums[i]);
                // update the count
                info[0]++;
                // update the last position
                info[2] = i;
            }
        }

        for(Integer num: infos.keySet()){
            // get the nums info
            int[] numInfo = infos.get(num);
            // find the max count
            if(numInfo[0]>count){
                minLen = numInfo[2] - numInfo[1] + 1;
                count = numInfo[0];
            }else if(numInfo[0] == count){
                // find the min length in the max nums
                minLen = Math.min(minLen, numInfo[2] - numInfo[1] + 1);
            }
        }
        return minLen;
    }
}

思路： 本题的关键点是能否把题目的意思做一个转换，进行哈希表的建模，主要思考过程如下：

  1. Number of Submatrices That Sum to Target

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1’, y1’, x2’, y2’) are different if they have some coordinate that is different: for example, if x1 != x1’.

Example 1:

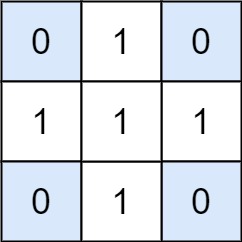
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Example 3:

Input: matrix = [[904]], target = 0
Output: 0

Constraints:

class Solution {

    public int numSubmatrixSumTarget(int[][] matrix, int target) {
        // 获得矩阵的长m和宽n
        int m = matrix.length;
        int n = matrix[0].length;
        int ans = 0;
        for(int i=0;i<m;i++){
            // 对于每行，new一个数组，上边界
            int[] nums = new int[n];
            for(int j=i;j<m;j++){
                for(int c=0;c<n;c++){
                    // 对于上边界的每行，获得下边界的行，在这个下边界的j行里面，把每列都加起来
                    nums[c] += matrix[j][c];// 更新每列的元素和
                }
                ans +=  checkSubmatrix(nums,target);
            }
        }
        return ans;
    }

    int checkSubmatrix(int[]nums,int k){
        Map<Integer,Integer> map = new HashMap<>();
        // 比较关键的点，是0，0的找0的可能性，是3种可能性，除了和是0，自身也会触发两次map值+1,所以是3
        map.put(0,1);
        int count = 0,pre = 0;
        for(int x: nums){
            pre += x;
            int res = pre - k;
            // 由于有0，所以可以这样相减看是否相等
            if(map.containsKey(res)){
                count += map.get(res);
            }
            map.put(pre,map.getOrDefault(pre,0)+1);
        }
        return count;
    }
}

先来看一个例子： 1 -1 -1 1 这个矩阵里面，需要找和为 0 的子矩阵。 可以很明确地得出答案：

第一行：1，-1，是一个答案 第二行，-1，1，是一个答案 第一列, 1,-1，是一个答案 第二列：-1，1，是一个答案 总体 2*2 的矩阵，本身是一个答案

解题思路：

这道题目需要确认如何可以一个不漏地把所有的子矩阵放入比较函数取比较，可以基于以下这几个思路：

设定一个上边界，对于每一个上边界，开辟一个数组，这个数组里面，保存所有以这个上边界和一会要遍历的下边界为上下行，所有列上的数值的和为元素的值。 举个例子：

  1. Group Anagrams

Given an array of strings strs, group the anagrams together. You can return the answer in any order.

An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.

Example 1:

Input: strs = ["eat","tea","tan","ate","nat","bat"]
Output: [["bat"],["nat","tan"],["ate","eat","tea"]]

Example 2:

Input: strs = [""]
Output: [[""]]

Example 3:

Input: strs = ["a"]
Output: [["a"]]

Constraints:

import java.util.*;


class Solution {
    Map<String, List<String>> groups = new HashMap();
    public List<List<String>> groupAnagrams(String[] strs) {
        for(String str: strs){
            char[] copyChar = str.toCharArray();
            Arrays.sort(copyChar);
            String key = Arrays.toString(copyChar);
            if(!groups.containsKey(key)){
                List<String> value = new ArrayList<>();
                value.add(str);
                groups.put(key,value);
            }else {
                groups.get(key).add(str);
            }
        }
        return new ArrayList<>(groups.values());
    }
}

思路：

分组就是哈希

  1. Substring with Concatenation of All Words

You are given a string s and an array of strings words. All the strings of words are of the same length.

A concatenated substring in s is a substring that contains all the strings of any permutation of words concatenated.

Example 1:

Input: s = "barfoothefoobarman", words = ["foo","bar"]
Output: [0,9]
Explanation: Since words.length == 2 and words[i].length == 3, the concatenated substring has to be of length 6.
The substring starting at 0 is "barfoo". It is the concatenation of ["bar","foo"] which is a permutation of words.
The substring starting at 9 is "foobar". It is the concatenation of ["foo","bar"] which is a permutation of words.
The output order does not matter. Returning [9,0] is fine too.

Example 2:

Input: s = "wordgoodgoodgoodbestword", words = ["word","good","best","word"]
Output: []
Explanation: Since words.length == 4 and words[i].length == 4, the concatenated substring has to be of length 16.
There is no substring of length 16 is s that is equal to the concatenation of any permutation of words.
We return an empty array.

Example 3:

Input: s = "barfoofoobarthefoobarman", words = ["bar","foo","the"]
Output: [6,9,12]
Explanation: Since words.length == 3 and words[i].length == 3, the concatenated substring has to be of length 9.
The substring starting at 6 is "foobarthe". It is the concatenation of ["foo","bar","the"] which is a permutation of words.
The substring starting at 9 is "barthefoo". It is the concatenation of ["bar","the","foo"] which is a permutation of words.
The substring starting at 12 is "thefoobar". It is the concatenation of ["the","foo","bar"] which is a permutation of words.

Constraints:

class Solution {

    int wordLength = 0;
    public List<Integer> findSubstring(String s, String[] words) {
        List<Integer> ans = new ArrayList<>();
        Map<String, Integer> wordsMap = new HashMap<>();
        int wto = 0;

        for (String word : words) {
            wto += word.length();
            wordLength = word.length();
            if (!wordsMap.containsKey(word)) {
                wordsMap.put(word, 1);
            } else {
                int count = wordsMap.get(word) + 1;
                wordsMap.put(word, count);
            }
        }

        //Note: the wto + i is less and equals the s.length, as the substring function can not get the end element
        for (int i = 0; wto + i <= s.length(); i++) {
            if (vaildEquals(s.substring(i, i + wto), wordsMap)) {
                ans.add(i);
            }
        }
        return ans;
    }

    private boolean vaildEquals(String substring, Map<String, Integer> wordsMap) {
        Map<String, Integer> strsMap = new HashMap<>();
        for (int i = 0; i < substring.length(); i += wordLength) {
            String word = substring.substring(i, i + wordLength);
            if (!strsMap.containsKey(word)) {
                strsMap.put(word, 1);
            } else {
                int count = strsMap.get(word) + 1;
                strsMap.put(word, count);
            }
        }
        return twoMapEquals(wordsMap, strsMap) && twoMapEquals(strsMap, wordsMap);
    }

    private boolean twoMapEquals(Map<String, Integer> oneMap, Map<String, Integer> twoMap) {
        for (Map.Entry<String, Integer> en :
                oneMap.entrySet()) {
            String key = en.getKey();
            Integer value = en.getValue();
            if (!twoMap.containsKey(key) || twoMap.get(key).intValue() != value.intValue()) {
                return false;
            }
        }
        return true;
    }
}
Share on