It’s all about datastruct and algorithm.
Table of contents
Open Table of contents
Stack
LIFO data structure. Last-In First-Out, stores objects into a sort of “vertical tower” push() to add to the top; pop() to remove from the top.
Using document
Stack<String> stack = new Stack<String>();
// add a element to top
stack.push("Hello");
stack.push("Minecraft");
// remove the top element
stack.pop();
// see the top element
stack.peek();
// search a element in the stack, return 1 to stack's size position
// if not found return -1.
stack.search("Minecraft");
stack.isEmpty();
Uses of stacks?
- undo/redo features in text editors
- moving back/forward through browser history
- backtracking algorithms (maze, file directories)
- calling functions (call stack)
Queue
FIFO data structure. First-In First-Out, A collection designed for holding elements prior to processing. Linear data structure. add() = enqueue, offer(); remove = dequeue, poll().
Queue<String> queue = new LinkedList<String>();
// Inserts element into this queue
queue.offer("Karen");
queue.offer("Chad");
queue.peek();
queue.poll();
queue.isEmpty();
queue.size();
queue.contains("Karen")
Uses of queue?
- Keyboard Buffer (letters should appear on the screen in the order they are pressed)
- Printer Queue (Print jobs should be completed in order)
- Used in LinkedLists, PriorityQueues, Breadth-first search
Priority Queue
A FIFO data structure that serves elements with the highest priorities first before elements with lower priority.
// 2.5, 3.0, 4.0
Queue<Double> queue = new PriorityQueue<>();
// 4.0, 3.0, 2.5
//Queue<Double> queue = new PriorityQueue<>(Collections.reverseOrder());
queue.offer(3.0);
queue.offer(2.5);
queue.offer(4.0);
while(!queue.isEmpty())){
System.out.println(queue.poll());
}
LinkedList
stores Nodes in 2 parts(data + address), Nodes are in non-consecutive memory locations, Elements are linked using pointers.
Advantages?
- Dynamic Data Structure (allocates needed memory while running)
- Insertion and Deletion of Nodes is easy. O(1)
- No/Low memory waste
Disadvantage?
- Greater memory usage (additional pointer)
- No random access of elements (no index [i])
- Accessing/Searching elements is more time consuming. O(n)
Uses?
- implement Stacks/Queues
- GPS navigation
- music playlist
LinkedList<String> linkedList = new LinkedList<String>();
// as a stack
linkedList.push("A");
linkedList.push("B");
linkedList.push("C");
linkedList.push("D");
linkedList.pop();
// as a queue
linkedList.offer("A");
linkedList.offer("B");
linkedList.offer("C");
linkedList.offer("D");
linkedList.poll();
// as link list
linkedList.add(4,"E");
linkedList.remove("E");
linkedList.peekFirst();
linkedList.peekLast();
linkedList.addFirst("0");
linkedList.addLast("G");Dynamic Array
Java = ArrayList; C++ = Vector; JavaScript = Array; Python = List;
Advantages
- Random access of elements O(1)
- Good locality of reference and data cache utilization
- Easy to insert/delete at the end
Disadvantages
- Wastes more memory
- Shifting elements is time consuming O(n)
- Expanding/Shrinking the array is time consuming O(n)
ArrayList<String> list = new ArrayList<>();
list.add("A");
list.add("B");
list.add("C");
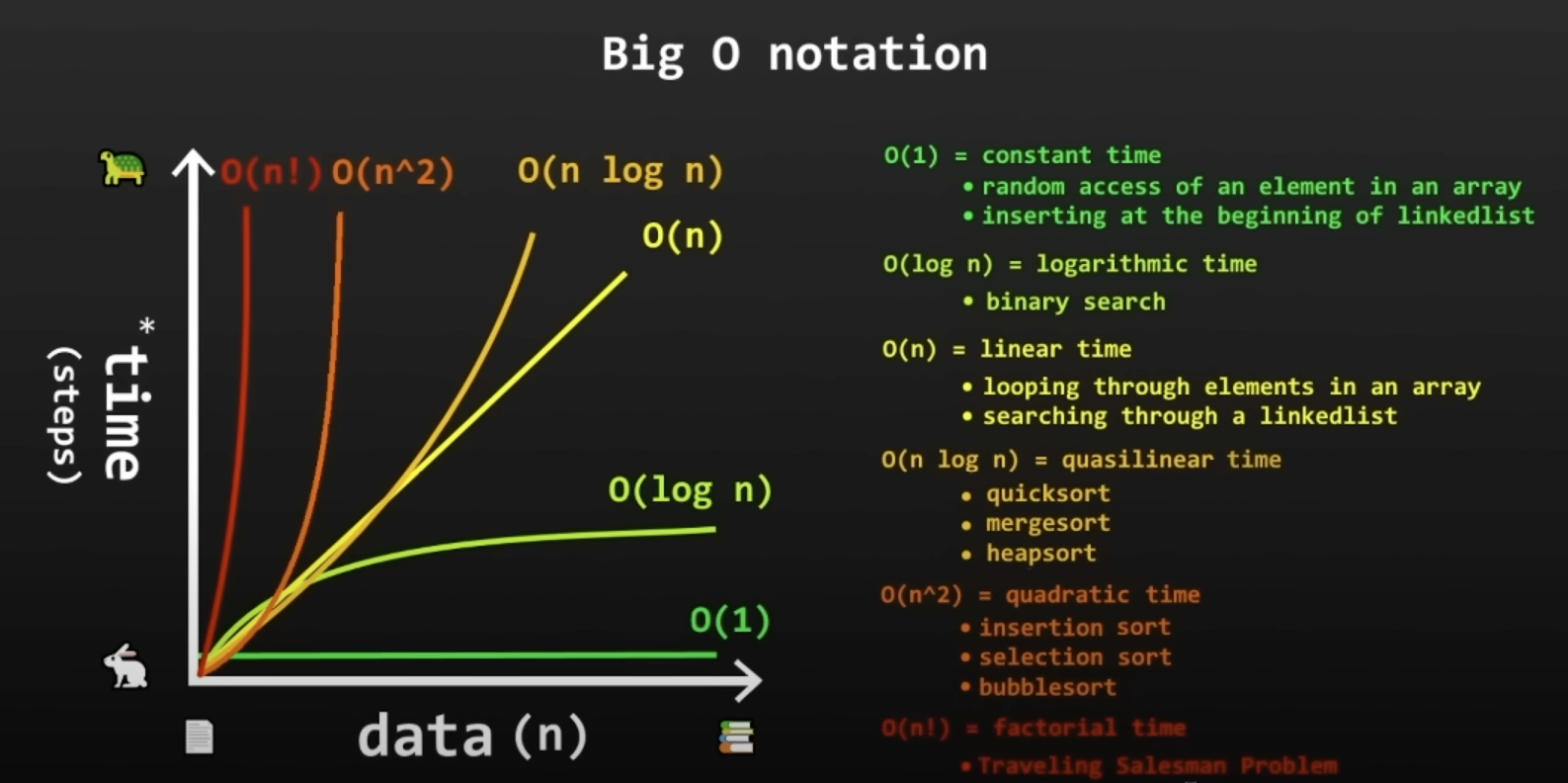
list.add("D");Big O notation
“How code slows as data grows.”
- Describes the performance of an algorithm as the amount of data increases
- Machine independent (# of steps to completion)
- Ignore smaller operations O(n+1) -> O(n)
Linear search
Iterate through a collection one element at a time
- runtime complexity: O(n)
Disadvantage
Slow for large data sets
Advantages
- Fast for searches of small to medium data sets
- Does not need to sorted
- Useful for data structures that do not have random access (Linked List)
Binary search
Search algorithm that finds the position of a target value within a sorted array. Half of the array is eliminated during each “step”;
int array[] = new int[100];
int target = 42;
for(int i=0; i< 100;i++){
array[i] = i;
}
int index = Arrays.binarySearch(array,tartget);public int binarySearch(int[] array, int target){
int low =0;
int high = array.length - 1;
while(low <= high){
int middle = low + (high - low)/2;
int value = array[middle];
if(value < target){
low = middle + 1;
}else if(value > target){
high = middle - 1;
}else{
return middle;// target found
}
}
return -1;// target not found
}Interpolation search
Improvement over binary search best used for “uniformly” distributed data “guesses” where a value might be based on calculated probe results, if probe is incorrect, search area is narrowed, and a new probe is calculated
- average case: O(log(log(n)))
- worst case: O(n) [values increase exponentially]
int [] array = {1,2,3,4,5,6,7,8,9};
int index = interpolationSearch(array, 8);
public int interpolationSearch(int[] array, int value){
int high = array.length - 1;
int low = 0;
while(value >= array[low] && value <= array[high] && low <= high){
int probe =low + (high - low) * (value - array[low]) /(array[high] - array[low]);
if(array[probe] == value){
return probe;
}esle if(array[probe] < value){
low = probe + 1;
}else{
high = probe -1;
}
}
return -1;
}Bubble sort
Pairs of adjacent elements are compared, and the elements swapped if they are not in order.
- Quadratic time O(n^2)
- small data set = okay-ish
- large data set = bad
public void bubbleSort(int[] array){
for(int i =0 ;i< array.length - 1; i++){
for(int j=0;j < array.length - 1 - i;j++){
if(array[j] > array[j+1]){
int temp = array[j];
array[j] = array[j+1]
array[j+1] = temp;
}
}
}
}Selection sort
search throgh an array and keep track of the minimum value during each interation, At the end of each iteration, we swap variables.
- Quadratic time O(n^2)
- small data set = okay
- large data set = BAD
public void selectionSort(int[] array){
for(int i = 0;i< array.length - 1;i++){
int min = i;
for(int j=i+1;j< array.length;j++){
if(array[min] > array[j]) {
min = j;
}
}
int temp = array[i];
array[i] = array[min];
array[min] = temp;
}
}Insertion sort
After comaring elements to the left shift elements to the right to make room to insert a value
- Quadratic time O(n^2)
- small data set = decent
- large data set = BAD
Less step than Bubble sort, Best case is O(n) compared to Selection Sort O(n^2)
public void insertionSort(int[] array){
for(int i=1;i<array.lenght;i++){
int temp = array[i];
int j = i-1;
while(j >=0 && array[j]>temp){
array[j+1] = array[j];
j--;
}
array[j+1] = temp;
}
}Recursion
When a thing is defined in terms of itself. - Wikipedia. Apply the result of a procedure, to a procedure. A recursive method calls itself. Can be a substitute for iteration.
Divide a problem into sub-problems of the same type as the original. Commonly used with advanced sorting algorithms and navigating trees.
Advantages
- easier to read/write
- easier to debug
Disadvantage
- sometimes slower
- uses more memory
| iteration | recursion | |
|---|---|---|
| implemention | uses loops | calls iteself |
| state | control index (int steps = 0) | parameter values walk(int steps) |
| progression | moves toward value in condition | converge towards base case |
| termination | index satisfies condition | base case = true |
| size | more code less memory | less code more momery |
| speed | faster | slower |
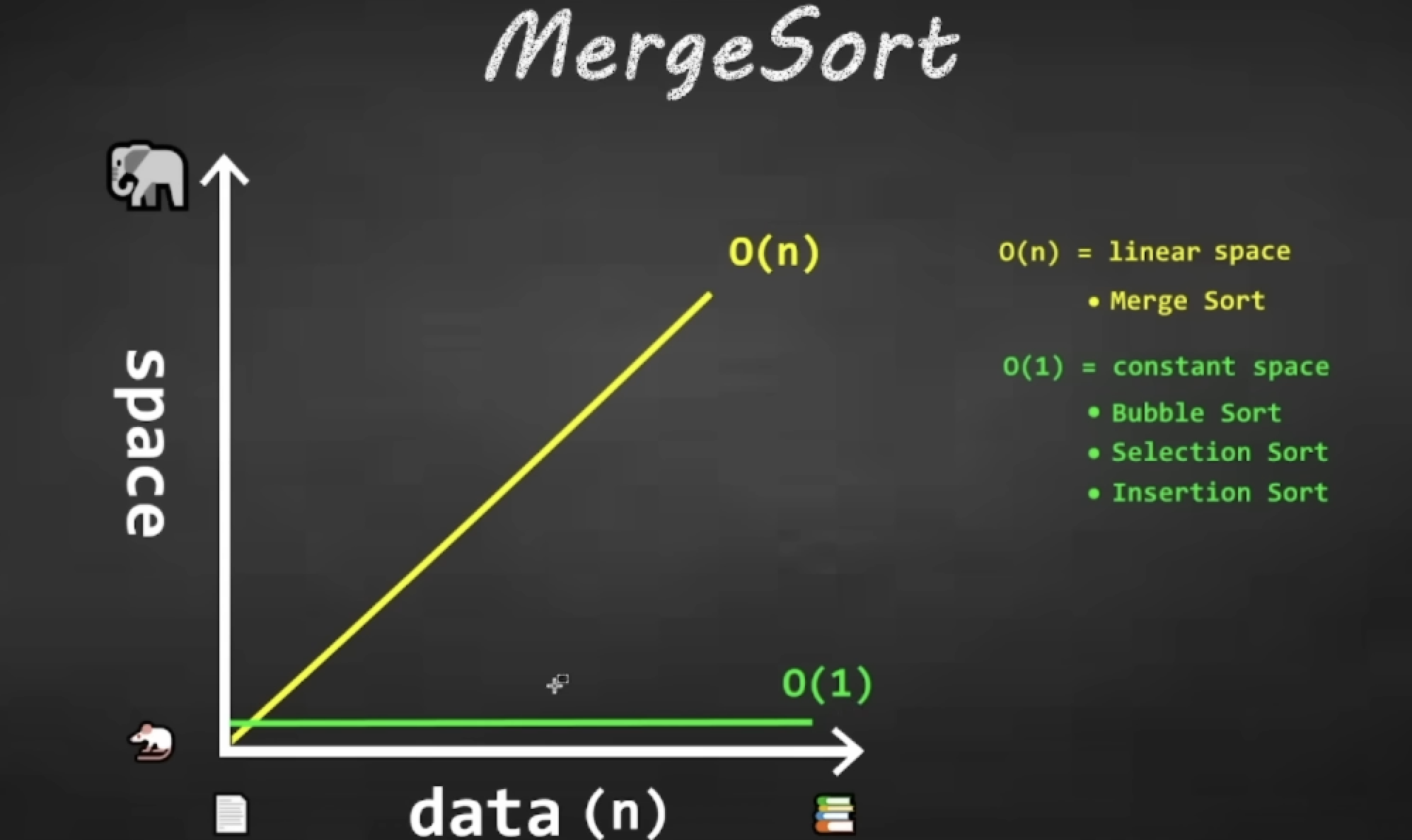
Merge sort
recursively divide array in 2, sort, re-combine.
- run-time complexity = O(nlog(n))
- space complexity = O(n);
public void mergeSort(int[] array){
int length = array.length;
if(length<=1) return; // base case
int middle = length / 2;
int[] leftArray = new int[middle];
int[] rightArray = new int[length-middle];
int i=0,l=0,r=0// indices
// copy elements to right and left array
for(;i<length;i++){
if(i<middle){
leftArray[l] = array[i];
l++
}else{
rightArray[r] = array[i];
r++;
}
}
mergeSort(leftArray):
mergeSort(rightArray);
// merge
merge(leftArray,rightArray,array);
}
public void merge(int[] leftArray, int[] rightArray, int[] array){
int leftSize = leftArray.length;
int rightSize = rightArray.length;
int i = 0, l = 0, r = 0; // indices
//check the conditions for merging
while(l < leftSize && r < rightSize){
if(leftArray[l] < rightArray[r]){
array[i] = leftArray[l];
i++;
l++;
}else{
array[i] = rightArray[r];
i++;
r++;
}
}
while(l < leftSize){
array[i] = leftArray[l];
i++;
l++;
}
while(r < rightSize){
array[i] = rightArray[r];
i++;
r++;
}
}Quick sort
Moves smaller elements to left of a pivot. recursively divide array in 2 partitions
- run-time complexity = Best case O(n(log(n))). Average case O(nlog(n)), worst case O(n^2) if already sorted
- space complexity = O(log(n)) due to recursion
public void quickSort(int[] array, int start, int end) {
if(end <= start) return;// base case
int pivotIndex = partition(array, start, end);
quickSort(array, start,pivotIndex-1);
quickSort(array,pivotIndex+1,end);
}
public int partition(int[] array, int start, int end) {
int pivot = array[end];
int i = start - 1;
for(int j = start; j< end;j++){
if(array[j] < pivot){
i++;
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// deal with the end element
i++;
int temp = array[i];
array[i] = array[end];
array[end] = temp;
return i;
}Hashtable
A data structure that stores unique keys to values. Each key/value pair is known as an Entry.
- FAST insertion, look up, deletion of key/value Pairs
- Not ideal for small data sets, great with large data sets
-
hashing = takes a key and computers an integer (formula will vary based on key& data type), In a Hashtable, we use the hash % capacity to calculate an index number
key.hashCode() % capcity = index -
bucket = an indexed storage location for one or more Entries can store multiple Entries in case of a collision(linked similarly a LinkedList)
-
collision = hash function generates the same index for more than one key
-
less collisions = more efficiency
- Runtime complexity: Best case O(1), Worst case O(n)
Undirected Graph
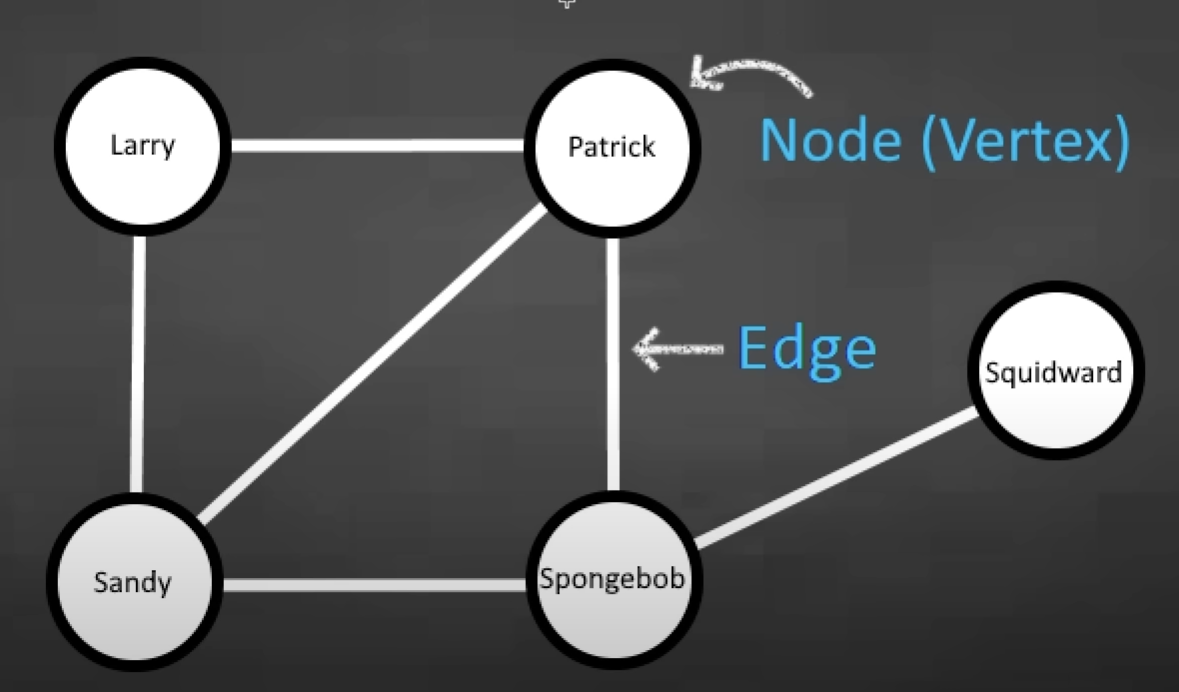
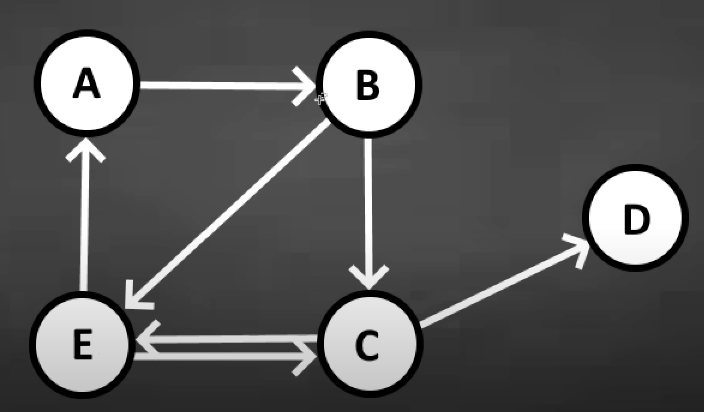
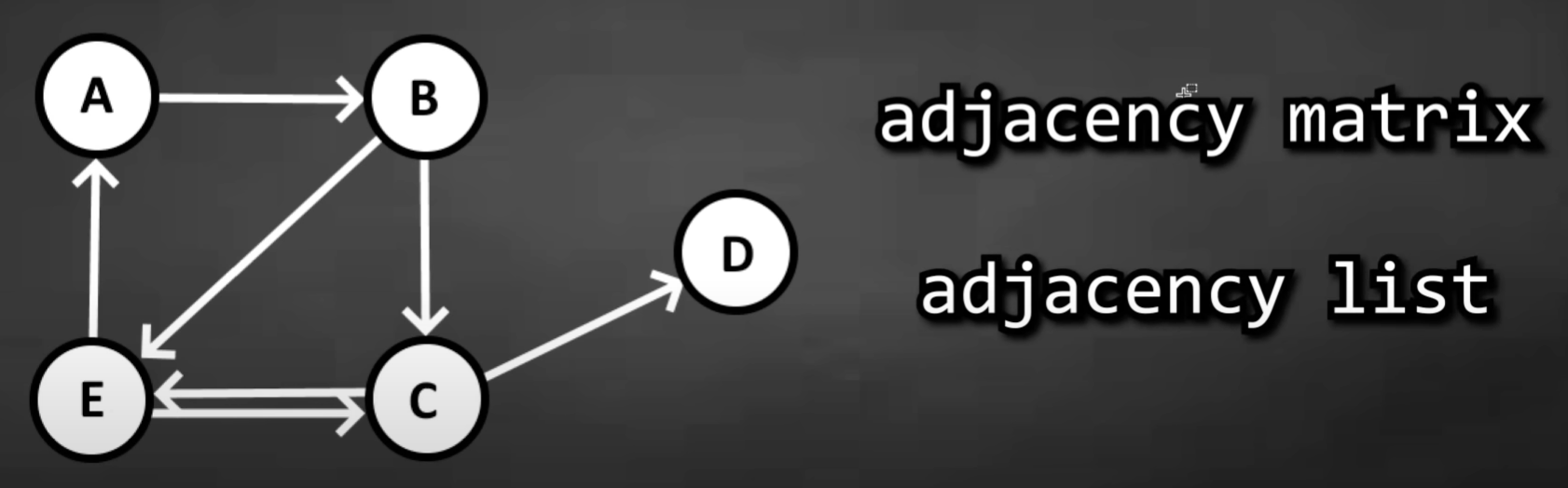
Adjacency Matrix
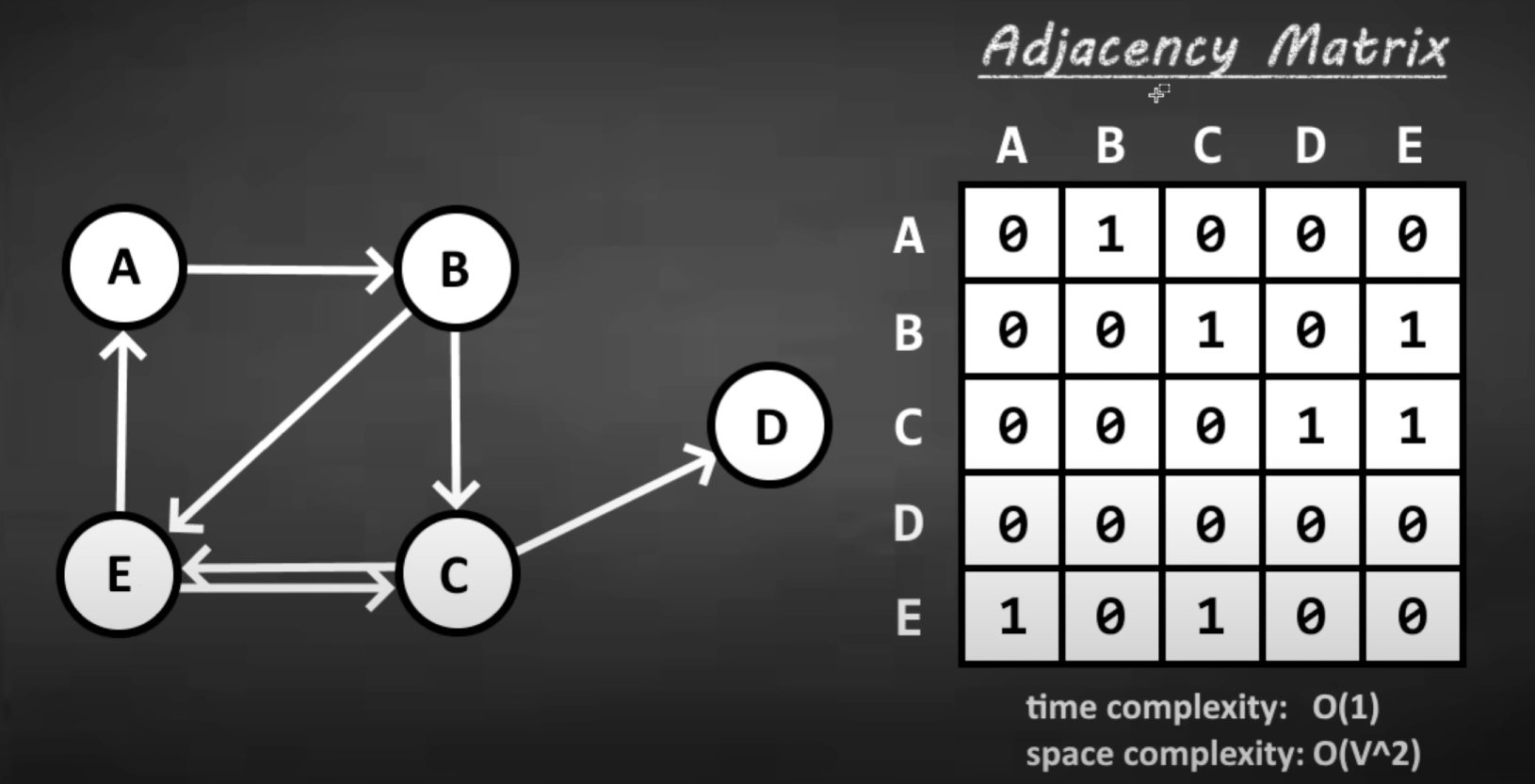
A 2D array to store 1’s/0’s to represent edges, # of rows = # of unique nodes; # of columns = # of unique nodes
- runtime complexity to check an Edge: O(1)
- space complexity: O(v^2)
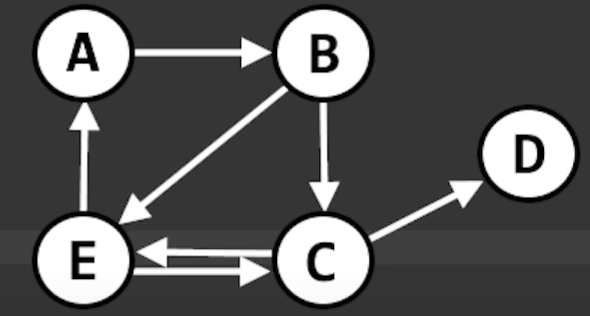
public class Node {
char data;
Node(char data){
this.data = data;
}
}
public class Graph{
ArrayList<Node> nodes;
int[][] matrix;
Graph(int size){
nodes = new ArrayList<>();
matrix = new int[size][size];
}
public void addNode(Node node){
nodes.add(node);
}
public void addEdge(int src, int dst){
matrix[src][dst] = 1;
}
public boolean checkEdge(int src, int dst){
return matrix[src][dst] == 1;
}
public void print(){
System.out.print(" ");
for(Node node: nodes){
System.out.print(node.data+ " ");
}
System.out.println();
for(int i =0;i<matrix.length;i++){
System.out.print(nodes.get(i).data + " ");
for (int j=0; j<matrix[i].length;j++){
System.out.print(matrix[i][j] +" ");
}
System.out.println();
}
}
}
public class Main {
public static void main(String[] arg){
Graph graph = new Graph(5);
graph.addNode(new Node('A'));
graph.addNode(new Node('B'));
graph.addNode(new Node('C'));
graph.addNode(new Node('D'));
graph.addNode(new Node('E'));
graph.addEdge(0,1);
graph.addEdge(1,2);
graph.addEdge(1,4);
graph.addEdge(2,3);
graph.addEdge(2,4);
graph.addEdge(4,2);
graph.addEdge(4,0);
graph.print();
System.out.println(graph.checkEdge(1,4));
}
}Adjacency List
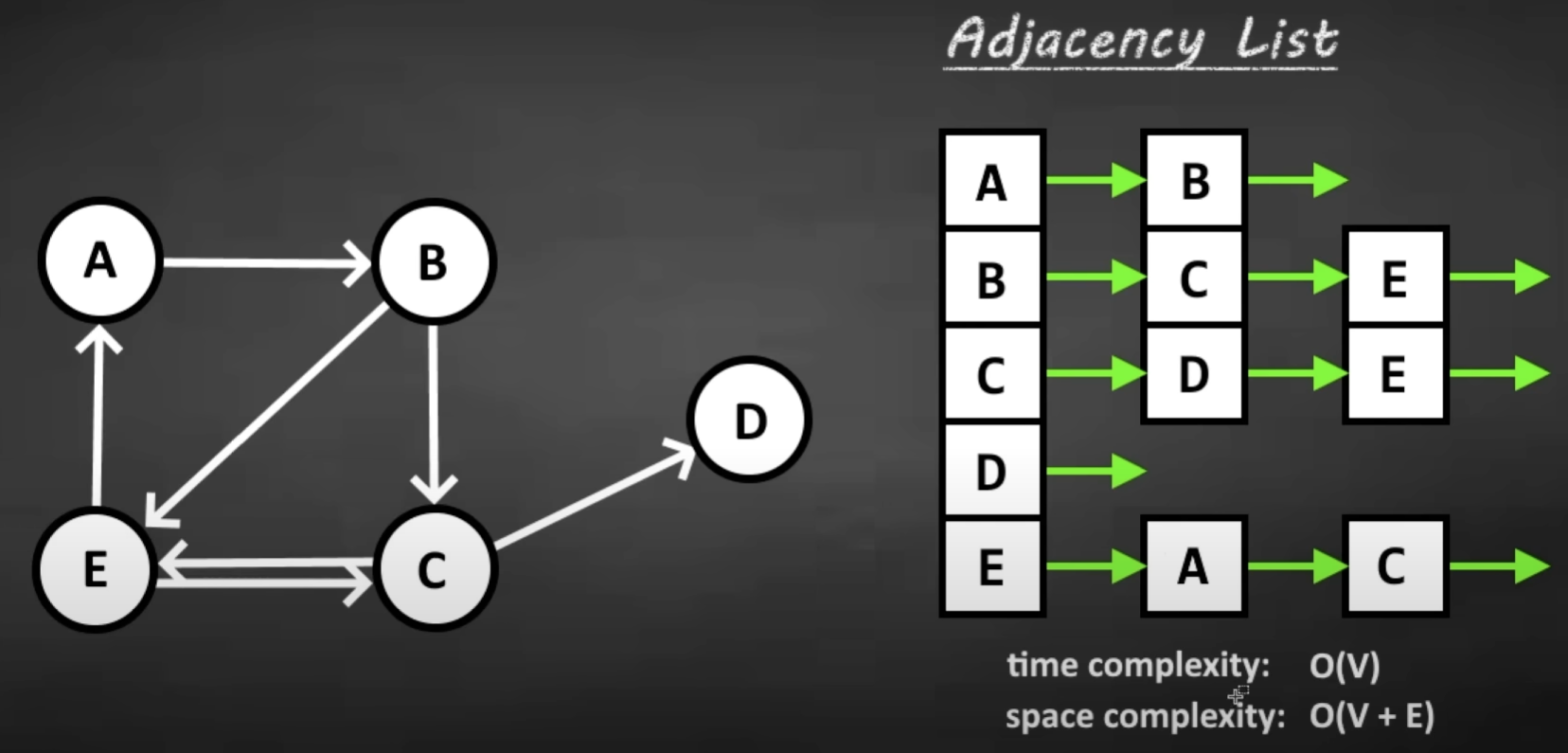
An array/arraylist of linkedlists. Each LinkedList has a unique node at the head. All adjacent neighbors to that node are add to that node’s linkedlist.
- runtime complexity to check an Edge: O(v)
- space complexity: O(v+e)
public class Node {
char data;
Node(char data){
this.data = data;
}
}
public class Graph{
ArrayList<LinkedList<Node>> alist;
Graph() {
alist = new ArrayList<>();
}
public void addNode(Node node) {
LinkedList<Node> currentList = new LinkedList<Node>();
currentList.add(node);
alist.add(currentList);
}
public void addEdge(int src, int dst) {
LinkedList<Node> currentList = alist.get(src);
Node dstNode = alist.get(dst).get(0);
currentList.add(dstNode);
}
public boolean checkEdge(int src, int dst) {
LinkedList<Node> currentList = alist.get(src);
Node dstNode = alist.get(dst).get(0);
for (Node node : currentList) {
if (node == dstNode) {
return true;
}
}
return false;
}
public void print() {
for (LinkedList<Node> currentList : alist) {
for (Node node : currentList) {
System.out.print(node.data + "->");
}
System.out.println();
}
}
}
public class Main {
public static void main(String[] arg){
Graph graph = new Graph(5);
graph.addNode(new Node('A'));
graph.addNode(new Node('B'));
graph.addNode(new Node('C'));
graph.addNode(new Node('D'));
graph.addNode(new Node('E'));
graph.addEdge(0,1);
graph.addEdge(1,2);
graph.addEdge(1,4);
graph.addEdge(2,3);
graph.addEdge(2,4);
graph.addEdge(4,2);
graph.addEdge(4,0);
graph.print();
System.out.println(graph.checkEdge(1,4));
}
}
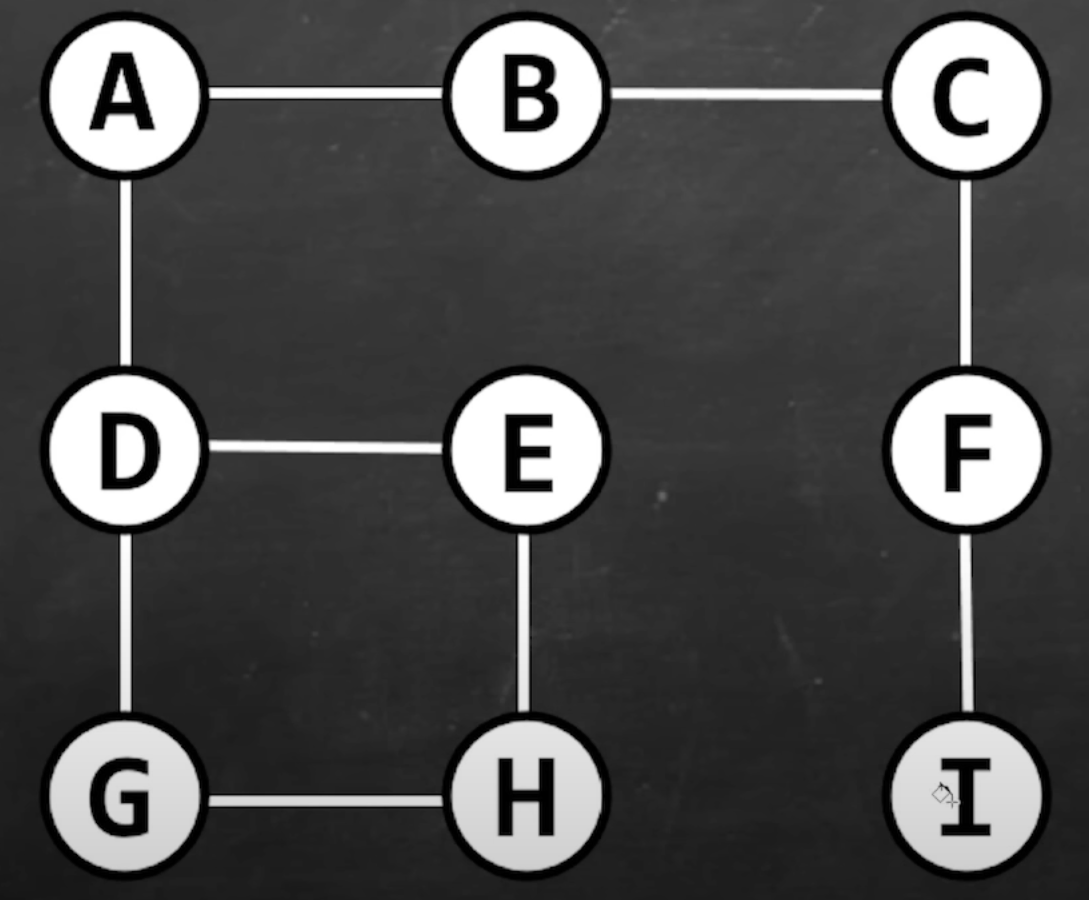
Depth First Search
DFS = a search algorithm for traversing a tree or graph data structure.
- Pick a route
- Keep going until you reach a dead end,or a previously visited node
- Backrtrack to last node that has unvisited adjacent neighbors
public class Node {
char data;
boolean visited;
Node(char data){
this.data = data;
}
}
public class Graph {
ArrayList<Node> nodes;
int[][] matrix;
Graph(int size){
nodes = new ArrayList<>();
matrix = new int[size][size];
}
public void addNode(Node node){
nodes.add(node);
}
public void addEdge(int src, int dst){
matrix[src][dst] = 1;
}
public boolean checkEdge(int src, int dst){
return matrix[src][dst] == 1;
}
public void print(){
System.out.print(" ");
for(Node node: nodes){
System.out.print(node.data+ " ");
}
System.out.println();
for(int i =0;i<matrix.length;i++){
System.out.print(nodes.get(i).data + " ");
for (int j=0; j<matrix[i].length;j++){
System.out.print(matrix[i][j] +" ");
}
System.out.println();
}
}
public void depthFirstSearch(int src){
boolean[] visited = new boolean[matrix.length];
dFSHelper(src,visited);
}
private void dFSHelper(int src, boolean[] visited) {
if(visited[src]) {
return;
}else{
visited[src] = true;
System.out.println(nodes.get(src).data + " = visited");
}
for (int i = 0; i < matrix[src].length; i++) {
if(matrix[src][i] == 1){
dFSHelper(i,visited);
}
}
}
}
public class Main {
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addNode(new Node('A'));
graph.addNode(new Node('B'));
graph.addNode(new Node('C'));
graph.addNode(new Node('D'));
graph.addNode(new Node('E'));
graph.addEdge(0,1);
graph.addEdge(1,2);
graph.addEdge(1,4);
graph.addEdge(2,3);
graph.addEdge(2,4);
graph.addEdge(4,2);
graph.addEdge(4,0);
graph.print();
System.out.println(graph.checkEdge(1,2));
graph.depthFirstSearch(3);
}
}Breadth First Search
BFS = a search algorithm for traversing a tree or graph data structure. This is done one “level” at a time, rather than one “branch” at a time.
public class Node {
char data;
boolean visited;
Node(char data){
this.data = data;
}
}
public class Graph {
ArrayList<Node> nodes;
int[][] matrix;
Graph(int size){
nodes = new ArrayList<>();
matrix = new int[size][size];
}
public void addNode(Node node){
nodes.add(node);
}
public void addEdge(int src, int dst){
matrix[src][dst] = 1;
}
public boolean checkEdge(int src, int dst){
return matrix[src][dst] == 1;
}
public void print(){
System.out.print(" ");
for(Node node: nodes){
System.out.print(node.data+ " ");
}
System.out.println();
for(int i =0;i<matrix.length;i++){
System.out.print(nodes.get(i).data + " ");
for (int j=0; j<matrix[i].length;j++){
System.out.print(matrix[i][j] +" ");
}
System.out.println();
}
}
public void breadthFirstSearch(int src){
Queue<Integer> queue = new LinkedList<>();
boolean[] visited = new boolean[matrix.length];
queue.offer(src);
visited[src] = true;
while(!queue.isEmpty()){
src = queue.poll();
System.out.println(nodes.get(src).data + " = visited");
for (int i = 0; i < matrix[src].length; i++) {
if(matrix[src][i] == 1 && !visited[i]){
queue.offer(i);
visited[i] = true;
}
}
}
}
}
public class Main {
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addNode(new Node('A'));
graph.addNode(new Node('B'));
graph.addNode(new Node('C'));
graph.addNode(new Node('D'));
graph.addNode(new Node('E'));
graph.addEdge(0,1);
graph.addEdge(1,2);
graph.addEdge(1,4);
graph.addEdge(2,3);
graph.addEdge(2,4);
graph.addEdge(4,2);
graph.addEdge(4,0);
graph.print();
System.out.println(graph.checkEdge(1,2));
graph.breadthFirstSearch(2);
}
}
Breadth FS = Traverse a graph level by level, Utilizes a Queue, Better if destination is on average close to start, Siblings are visited before children
Depth FS = Traverse a graph branch by branch, Utilizes a Stack, Better if destination is on average far from the start. children are visited before siblings, More popular for games/puzzles
Tree
tree = a non-linear data structure where nodes are organized in a hierarchy.
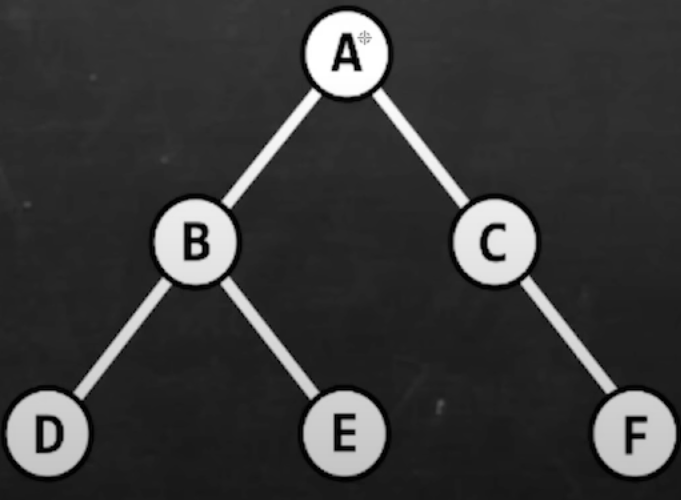
Uses
- File explorer
- Databases
- DNS
- HTML DOM
Binary search tree
A tree data structure, where each node is greater than its left child,but less than right.
Benefit: easy to locate a node when they are in this order
- time complexity: best case O(log(n)); worst case O(n)
- space complexity: O(n)
public class Node{
int data;
Node left;
Node right;
public Node(int data){
this.data = data;
}
}
public class BinarySearchTree {
Node root;
public void insert(Node node){
root = insertHelper(root, node);
}
private Node insertHelper(Node root, Node node) {
int data = node.data;
if(root == null){
root = node;
return root;
}else if(data < root.data){
root.left = insertHelper(root.left,node);
}else{
root.right = insertHelper(root.right,node);
}
return root;
}
public void display(){
displayHelper(root);
}
private void displayHelper(Node root) {
if(root != null){
displayHelper(root.left);
System.out.println(root.data);
displayHelper(root.right);
}
}
public boolean search(int data){
return searchHelper(root,data);
}
private boolean searchHelper(Node root, int data) {
if(root==null){
return false;
}
else if(root.data == data){
return true;
}
else if(root.data>data){
return searchHelper(root.left,data);
}else {
return searchHelper(root.right,data);
}
}
public void remove(int data){
if(search(data)){
removeHelper(root,data);
}else{
System.out.println(data + " could not be found!");
}
}
private Node removeHelper(Node root, int data) {
if (root == null){
return null;
}else if(data < root.data){
root.left = removeHelper(root.left, data);
}else if(data > root.data){
root.right = removeHelper(root.right,data);
}else { // node found
if(root.left == null && root.right == null){ // leaf node
root = null;
}else if(root.right != null){ // find a successor to replace this node
root.data = successor(root);
root.right = removeHelper(root.right,root.data);
}else{// find a predecessor to replace this node
root.data = predecessor(root);
root.left = removeHelper(root.left,root.data);
}
}
return root;
}
private int predecessor(Node root) { // find greatest value below the left child of this root node
root = root.left;
while(root.right != null){
root = root.right;
}
return root.data;
}
private int successor(Node root) { // find least value below the right child of this root node
root = root.right;
while(root.left != null){
root = root.left;
}
return root.data;
}
}
public class Main {
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
tree.insert(new Node(5));
tree.insert(new Node(1));
tree.insert(new Node(9));
tree.insert(new Node(2));
tree.insert(new Node(7));
tree.insert(new Node(3));
tree.insert(new Node(6));
tree.insert(new Node(4));
tree.insert(new Node(8));
//tree.display();
System.out.println(tree.search(9));
tree.remove(5);
tree.display();
}
}